ノズルの圧力、口径、および流量の計算

ノズルの流量は、口径サイズと圧力に密接に関連しています。圧力または口径サイズが増加すると流量も増加しますが、この増加は線形的ではありません。実際、同じ圧力下では流量は口径直径の二乗に比例します。同様に、口径サイズが一定の場合、流量は圧力の平方根に比例します。

LORRICの同一モデルのノズルには、さまざまな流量オプションが用意されています。これは、同じノズルに対して異なる口径サイズを設計し、それに適した圧力範囲を設定することで実現されています。言い換えると、顧客は流量コードと圧力を参照することで、要件に合ったノズル仕様を選択できます。

本記事では、流量、圧力、および口径サイズの関係を理解するためのガイドを提供します。

圧力が増加すると、流量は圧力の平方根に比例して増加します。では、なぜそうなるのでしょうか？ノズルの流量は次の式を使用して算出されます：

• では、圧力が増加すると流量はどのように変化するのでしょうか？
上記の式からわかるように：
圧力が増加すると流量も増加しますが、線形的ではなく、平方根の関係に従います。
例えば、圧力が2 barから8 bar（4倍）に増加した場合、流量は√4 = 2倍にしかなりません。
つまり、流量 Q は圧力差 ΔP の平方根に比例します。
このため、流量 Q と圧力 P の関係を次のように表現できます：
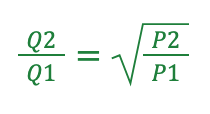
このように、流量と圧力差の関係を利用して値を簡単に計算できます。例えば、ノズルの運転条件（流量など）を変更する際、この式を使って必要な圧力変化を計算したり、逆に異なる圧力での流量を求めることができます。
• 1つのノズルで異なる圧力下での流量を計算したい場合、どうすれば良いですか？
例えば、あるノズルが3 barで流量が3.91 m³/sの場合、圧力が100 barのときの流量はどうなるでしょうか？

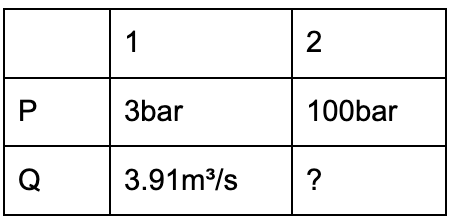
100 barでの流量（Q2）を求めるために、流量が圧力の平方根に比例することを考慮し、式に値を代入します：
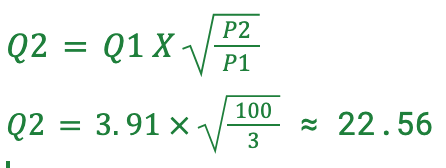
100 barの圧力下での流量は、約22.56 m³/sと計算されます。

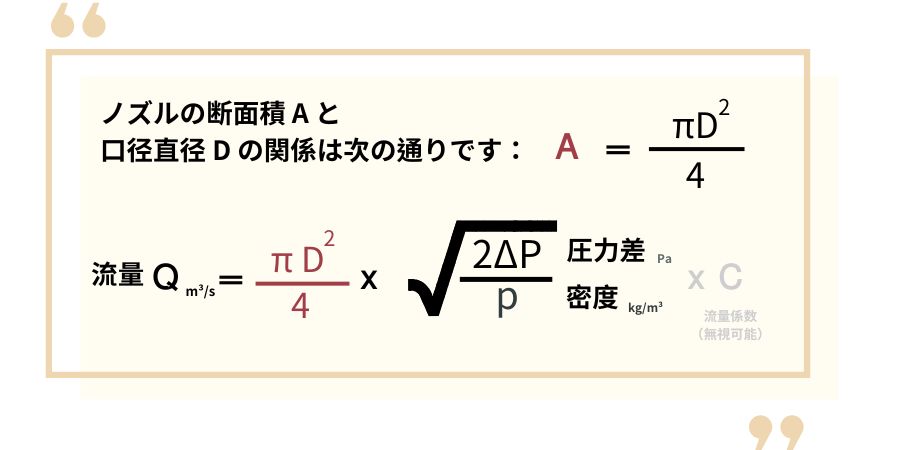
同じ圧力下では、流量 Q は口径直径 D^2 の二乗に比例することが観察できます。
流量が口径直径の二乗に比例するという仮定に基づき、次の式を使用して流量を計算できます：

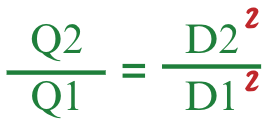
計算例：
同じ圧力条件下で、異なる口径サイズを持つノズルの流量をどのように計算するか？
例えば、口径直径が2 mmのとき、ノズルの流量が10 L/minの場合、口径直径が4 mmに増加した場合の流量はいくらになりますか？

既知の値を代入します：

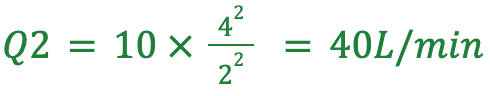
口径直径が4 mmの場合、ノズルの流量は約40 L/minと計算されます。

「口径直径がスプレー性能を決定するわけではない」
前述のセクションで述べたように、ノズルのスプレー性能は口径直径、圧力、流量など複数の要因によって影響を受けます。

非専門的なノズル販売プラットフォームでは、しばしば口径サイズだけを基準として仕様を提示します。しかし、実際にはノズルの流量やスプレー角度は口径サイズだけで決定されるものではありません。例えば、ファン型ノズルの楕円形のオリフィスでは、その直径を直感的に定義することが難しいです。同じ1 mmの口径直径を持つノズルであっても、流量、スプレー角度、衝撃分布は大きく異なる場合があります。

ノズルを設計する際、専門メーカーは顧客が求める性能を最優先に考慮します。当社のノズルは、スプレー角度と流量を圧力と対応付けた参照チャートを備えており、顧客が初期仕様を選定できるようにしています。使用中に期待したスプレー効果が得られない場合、すぐに口径サイズの増減を提案するのではなく、分布パターンを調査し、現場での問題を特定し、ノズルモデルの変更が結果を改善するかどうかを評価します。複数の要因を総合的に検討することで、顧客の期待するスプレー性能を実現することを目指しています。