노즐 압력, 구경 및 유량 계산

노즐의 유량은 구경 크기와 압력과 밀접한 관련이 있습니다. 압력이나 구경 크기가 증가하면 유량도 증가하지만, 이 증가는 선형적이지 않습니다. 실제로 동일한 압력 조건에서는 유량이 구경 직경의 제곱에 비례합니다. 마찬가지로, 구경 크기가 고정된 경우 유량은 압력의 제곱근에 비례합니다.  

LORRIC의 동일한 노즐 모델은 다양한 유량 옵션을 제공합니다. 이는 동일한 노즐에 대해 다른 구경 크기를 설계하고, 적합한 압력 범위를 조정함으로써 가능해집니다. 즉, 고객은 유량 코드와 압력을 참고하여 요구에 맞는 노즐 사양을 선택할 수 있습니다.  

이 글에서는 유량, 압력, 그리고 구경 크기 간의 관계를 독자들이 이해할 수 있도록 안내합니다.

압력이 증가하면 유량은 압력의 제곱근에 비례하여 증가합니다. 그런데 왜 이런 현상이 나타날까요? 노즐의 유량은 다음 공식을 사용하여 계산됩니다:

• 그래서 압력이 증가하면 유량은 어떻게 변할까요?
위 공식을 통해 알 수 있듯이:
압력이 증가하면 유량도 증가하지만, 선형적으로 증가하지 않고 제곱근 관계를 따릅니다.
예를 들어, 압력이 2 bar에서 8 bar로 (4배) 증가하면, 유량은 √4 = 2배만 증가합니다.
즉, 유량 Q는 압력 차 ΔP의 제곱근에 비례합니다.
따라서 유량 Q와 압력 P의 관계를 다음과 같이 설명할 수 있습니다:
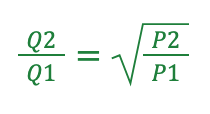
이러한 관계를 이용하여 유량과 압력 차를 계산할 수 있습니다. 예를 들어, 노즐의 작동 조건(예: 유량)을 변경할 때 이 공식을 사용하여 필요한 압력 변화를 계산하거나, 반대로 다양한 압력에서의 유량을 확인할 수 있습니다.
• 노즐의 유량을 다른 압력에서 계산하고 싶습니다. 어떻게 계산할 수 있을까요?
노즐의 유량이 3 bar에서 3.91 m³/s라고 가정해봅시다. 이 노즐의 압력이 100 bar일 때 유량은 얼마일까요?

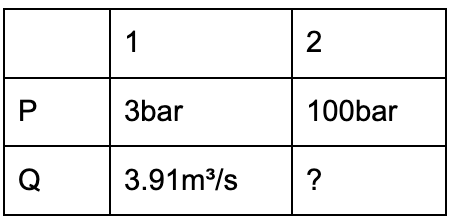
100 bar에서의 유량(Q2)을 구하기 위해, 유량이 압력의 제곱근에 비례한다는 것을 알고 공식을 사용해 값을 대입합니다:
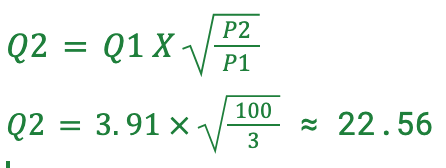
100 bar에서의 유량은 약 22.56 m³/s로 계산됩니다.

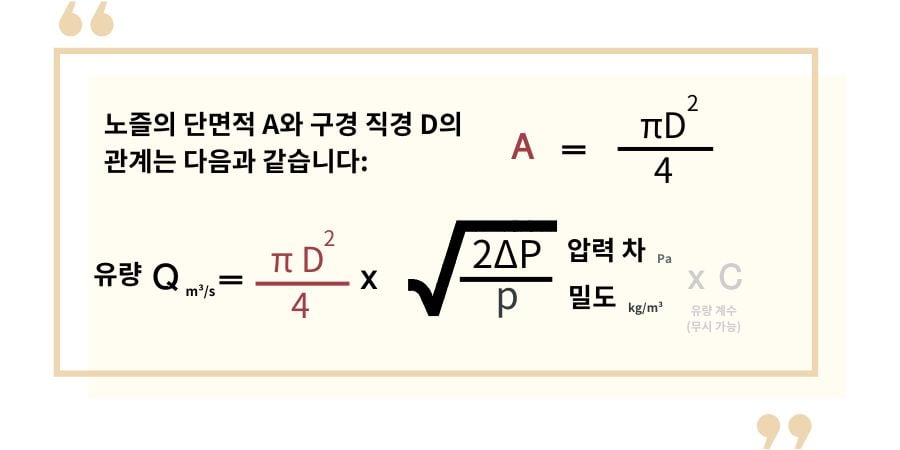
동일한 압력 하에서, 유량 Q는 구경 직경 D^2의 제곱에 비례한다는 것을 알 수 있습니다.
유량이 구경 직경의 제곱에 비례한다는 가정에 기반하여, 다음 공식을 사용해 유량을 계산할 수 있습니다:

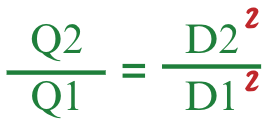
예제 계산:
동일한 압력 하에서, 다른 구경 크기를 가진 노즐의 유량을 어떻게 계산할 수 있을까요?
구경 직경이 2mm일 때 노즐의 유량이 10 L/min인 경우, 구경 직경이 4mm로 증가하면 유량은 얼마가 될까요?

알려진 값을 대입합니다:

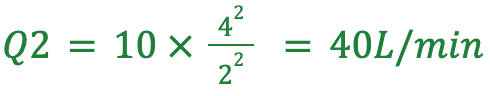
구경 직경이 4mm일 때, 노즐의 유량은 약 40 L/min으로 계산됩니다.

“구경 직경은 분사 성능을 결정하지 않습니다”
앞서 설명한 바와 같이, 노즐의 분사 성능은 구경 직경, 압력, 유량 등 여러 요인에 의해 영향을 받습니다.

비전문적인 노즐 판매 플랫폼에서는 종종 구경 크기만을 기준으로 사양을 제시합니다. 그러나 실제로 노즐의 유량과 분사 각도는 구경 크기만으로 결정되지 않습니다. 예를 들어, 팬형 노즐의 타원형 오리피스는 직경을 직관적으로 정의하기 어렵습니다. 동일한 1mm 구경을 가진 노즐이라도 유량, 분사 각도, 충격 분포는 크게 다를 수 있습니다.

전문 제조업체는 노즐 설계 시 고객이 원하는 성능을 최우선으로 고려합니다. 당사의 노즐은 분사 각도와 유량을 압력과 연결한 참조 차트를 제공하여 고객이 초기 사양을 선택할 수 있도록 돕습니다. 사용 중 원하는 분사 효과가 나오지 않을 경우, 바로 구경 크기를 조정하는 대신 분포 패턴을 조사하고, 현장에서 발생한 문제를 파악하며, 노즐 모델 변경이 결과를 개선할 수 있는지를 평가합니다. 여러 요인을 종합적으로 고려하여 고객이 기대하는 분사 성능을 달성하는 것이 목표입니다.