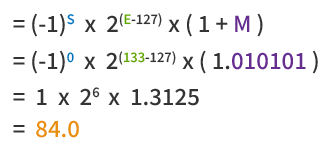1. What Is a Floating-Point Number?
A floating-point number is a way to represent decimals or extremely large numbers using a limited amount of memory. As Mitra (2017, para. 2) notes, "While integer operations are faster and free from rounding errors, integer types are not well-suited for representing fractions or values across an extreme range."
That’s where floating-point numbers come in—they allow us to handle continuous numerical data more effectively. They're especially useful in scientific calculations, such as representing physical constants or measuring distances on atomic or galactic scales. These types of values are difficult, if not impossible, to express with integers. That’s why virtually all modern programming languages support floating-point data types as a standard.
[1]
2. Floating-Point Representation
Floating-point numbers work similarly to scientific notation.
For example, the number 12345 in scientific notation is written as
1.2345 × 10⁴
Here, 1.2345 is called the fraction (or mantissa), and 4 is the exponent.
Scientific notation uses base 10 (decimal), while floating-point numbers use base 2 (binary).
Take the number 15 as an example:
| Integer (Decimal) |
Scientific Notation (Decimal) |
Floating-point (Binary) |
| 15 |
(1.5)10 × 101 |
(1.111)2 × 23 |
Example: Representing the number 15 as a floating-point value
Step 1: Convert 15 to binary
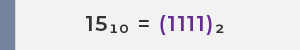
Step 2: Shift all significant digits of the mantissa to the right of the decimal point to form (1.XXXX)₂ × 2ⁿ
Move the decimal point three places to the left. To keep the value the same, raise base 2 to the power of 3
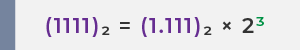
✅ Final Floating-Point Representation:
1 ) IEEE 754 Floating-Point Format
To avoid inconsistent floating-point results across different platforms, the IEEE (Institute of Electrical and Electronics Engineers) introduced the IEEE 754 standard in 1985. This standard has been widely adopted since the 1990s to define how floating-point numbers are represented and calculated (Wikipedia, 2024):
IEEE 754 defines:
- Storage formats for floating-point numbers (e.g., 32-bit Float32 and 64-bit Float64).
- Rules for floating-point operations (e.g., rounding modes, special values like NaN and infinity).
- Exceptional cases (e.g., overflow, underflow, and division by zero).
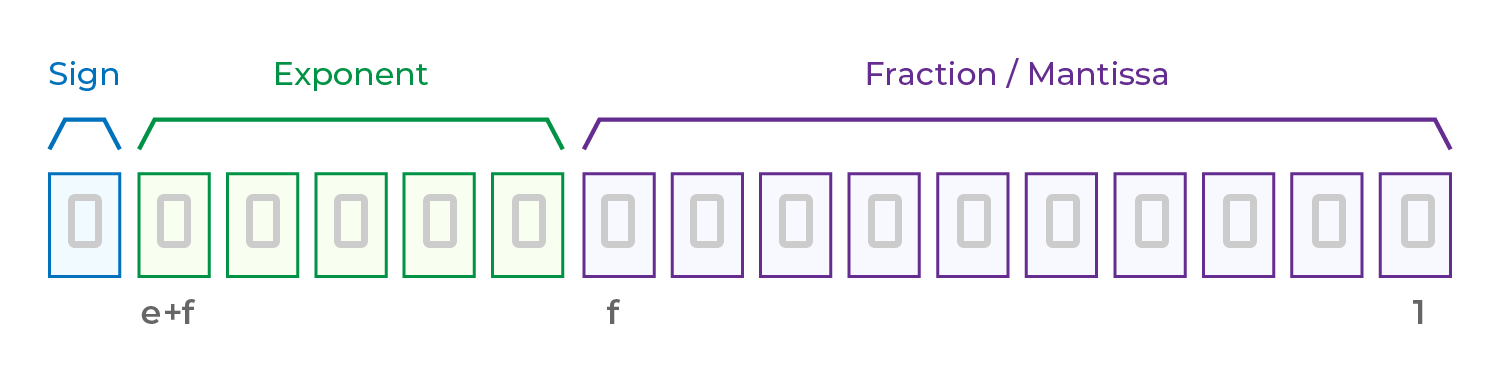
IEEE 754 specifies the structure of floating-point numbers as follows:
Value = (−1)sign × 2exponent × (1 + fraction)
Sign Bit: 1 bit, determines whether the number is positive or negative: 0 = positive / 1 = negative
Exponent Bias: Used to control the range of the value (as powers of 2), calculated as the exponent minus the bias.
Fraction (Mantissa): Represents "1 + fractional part" and stores the significant digits (similar to "1.XX" in scientific notation).
2 ) Floating-Point Precision: Float32 & Float64
The floating-point representation of
15 is
(1.111)₂ × 2³, written as
(−1)⁰ × 2³ × (1.111)₂
This follows the IEEE 754 normalized format. When computers store floating-point numbers, they encode them according to the IEEE 754 standard using either single precision (Float32) or double precision (Float64).
Single Precision
When storing a floating-point number, the leading 1 is implicit, so only the fractional part is saved instead of the full significand.
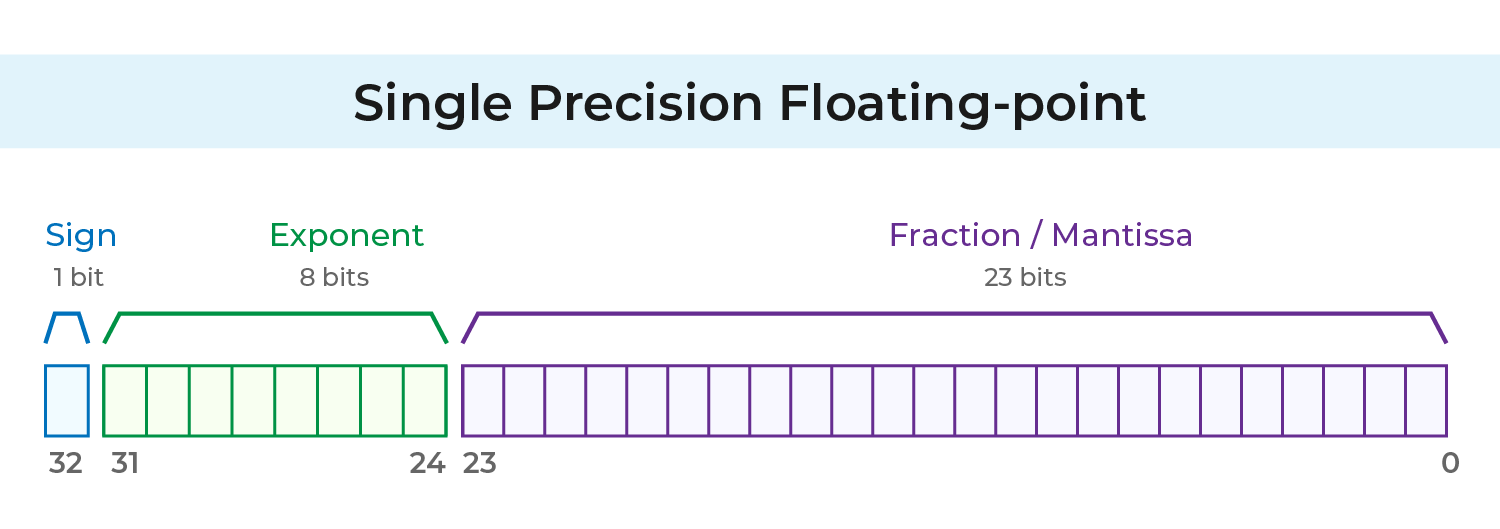
IEEE 754 single precision uses 32 bits in total:
1 bit: Sign bit
8 bits: Exponent (m)
23 bits: Fraction (f)
In single precision, the exponent is biased by 127 to avoid storing a negative sign. The computer stores
m + 127 instead of
m. Therefore, the maximum exponent value is 127, and the minimum is −126.
(Grainger College of Engineering, 2019)
* For calculation examples, please refer to the next section.
Double Precision
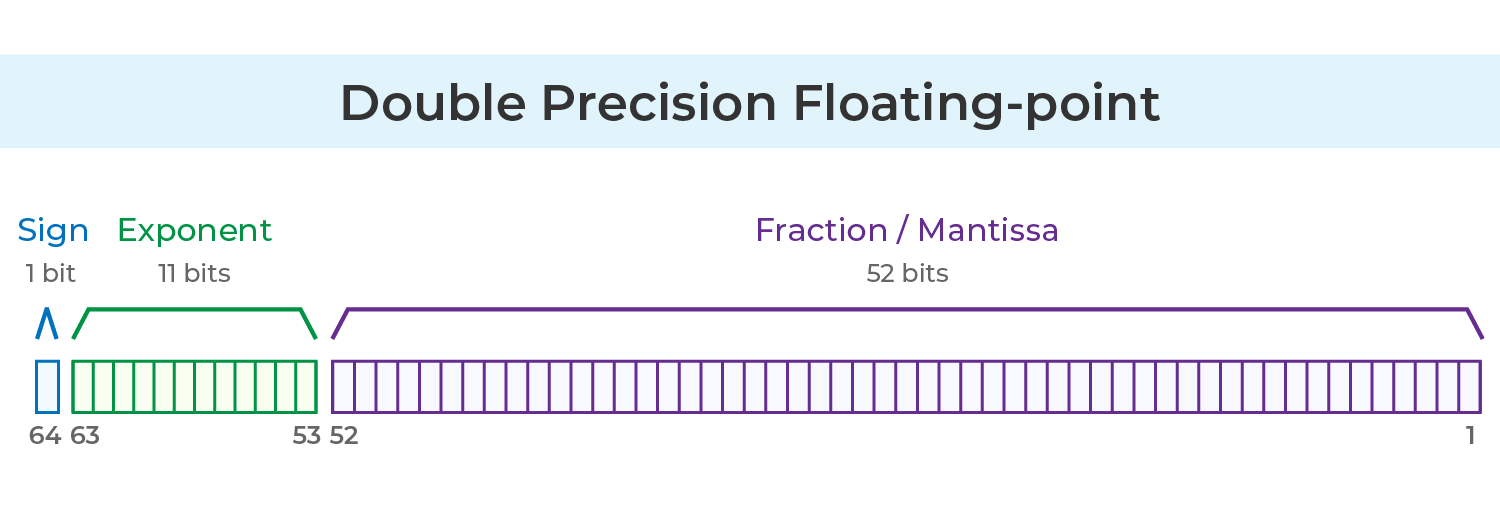
IEEE 754 double precision uses 64 bits in total:
1 bit: Sign bit
11 bits: Exponent (m)
52 bits: Fractional part (f)
In double precision, the exponent is biased by 1023 to avoid storing a negative sign. The computer stores
m + 1023 instead of
m. Therefore, the maximum exponent value is 1023, and the minimum is −1022.
(Grainger College of Engineering, 2019)
Float32 vs Float64 Feature Comparison
| Feature |
Float32 (Single Precision) |
Float64 (Double Precision) |
| Bit Length |
32 bits |
64 bits |
| Fraction Length |
23 bits (about 7–8 decimal digits) |
52 bits (about 15–16 decimal digits) |
| Exponent Length |
8 bits (bias: 127) |
11 bits (bias: 1023) |
| Value Range |
Approx. 10⁻³⁸ ~ 10³⁸ |
Approx. 10⁻³⁰⁸ ~ 10³⁰⁸ |
| Memory Usage |
4 bytes (32-bit) |
8 bytes (64-bit) |
| Performance |
Faster (ideal for graphics processing, AI training) |
Slower but more accurate (better for scientific computing) |
| Common Applications |
• Game development, graphics processing (GPU computing)
• Machine learning (e.g., mixed precision in TensorFlow)
• Large datasets with low precision requirements
|
• Scientific computing and simulations (e.g., weather forecasting, physics modeling)
• Financial calculations (to avoid rounding errors)
• High-precision numerical computing (e.g., engineering applications)
|
3. 32-bit Floating-Point Calculation Example
| Single Precision (Float32, 32-bit) Format |
| Component |
Bit Length |
Description |
| Sign Bit (S) |
1 bit |
0 (positive) |
| Exponent (E) |
8 bits |
3 + 127 = 130 = 10000010₂ |
| Fraction (M) |
23 bits |
11100000000000000000000 (omit the leading 1., store only 111) |
| Storage |
32 bits |
0 10000010 11100000000000000000000 |
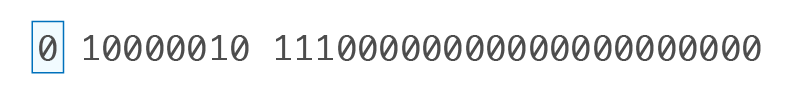• Sign Bit (S): 0
(−1)⁰ = 1 (indicates a positive number)
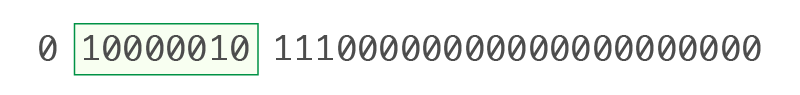• Exponent (E) (Bits 2–9): 10000010
Convert to decimal: 10000010₂ = 130₁₀
*IEEE 754 uses a bias value of 127
130 - 127 = 3
So, the exponent = 3, meaning 2³
(*IEEE 754 uses a bias to represent exponents. For single precision (32-bit), the exponent field uses 8 bits. According to the IEEE 754 definition, the bias is calculated as: Bias = 2⁸⁻¹ − 1 = 127)
• Fraction (M): 11100000000000000000000
According to IEEE 754, the fraction uses the normalized form “1 + fractional value,” so the actual value is: 1.11100000000000000000000₂
Convert to decimal:
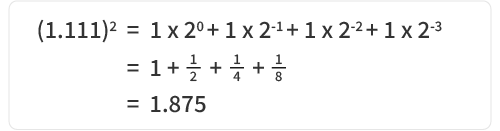
IEEE754 floating-point format is defined as:
4. Modbus Floating-Point Access and Conversion
In Modbus communication, data is stored in registers, with each register being 16 bits wide. However, representing a single-precision floating-point number requires 32 bits. To handle this within the Modbus architecture, data that exceeds 16 bits must span multiple consecutive register addresses. Therefore, a 32-bit float needs to occupy two adjacent registers.
The Modbus protocol specifies the use of Big-Endian format for transmitting multi-byte values. In Big-Endian order, the most significant byte is sent first. For example, the 16-bit hexadecimal value 0x1234 would be transmitted on the bus as 0x12 followed by 0x34. (Modbus Organization, 2006)
[4]
1 ) How Modbus Stores a 32-bit Floating-Point Number
How is the floating-point number 84.0 stored in Modbus?
• Convert to IEEE 754 single-precision floating-point format:
The IEEE 754 single-precision (32-bit) binary representation of 85.625 is:
01000010101010000000000000000000₂
• Convert to hexadecimal: 0x42A80000
• Storage in Modbus (Big-Endian format):
Since each Modbus register is 16 bits, a 32-bit float is split across two registers:
High register (first 16 bits): 0x42A8
Low register (last 16 bits): 0x0000
2 ) How to Decode Modbus Values Back into Floating-Point Numbers
Example:
Device Address (Slave ID): 0x01
Function Code: 0x03 (Read Holding Registers)
Starting Register Address: 0x1000
Number of Registers to Read: 0x0002 (since a 32-bit float occupies two 16-bit registers)
➤ Modbus Transmission Request (TX - Master sends data):
01 03 10 00 00 02 C5 CD
| Byte |
Description |
Value |
| 01 |
Device Address (Slave ID) |
0x01 |
| 03 |
Function Code (Read Holding Registers) |
0x03 |
| 10 00 |
Starting Address (0x1000) |
0x1000 |
| 00 02 |
Quantity of Registers (Read 2) |
0x0002 |
| C5 CD |
CRC-16 Checksum |
0xC5CD |
➤ Modbus Device Response (RX - Slave responds):
01 03 04 42 A8 00 00 79 32
| Byte |
Description |
Value |
| 01 |
Device Address (Slave ID) |
0x01 |
| 03 |
Function Code (Read Holding Registers) |
0x03 |
| 04 |
Byte Count |
0x04 (4 bytes = 32-bit) |
| 42 A8 |
High Register Value |
0x42A8 |
| 00 00 |
Low Register Value |
0x0000 |
| 79 32 |
CRC-16 Checksum |
0x7932 |
As shown, the merged register data is:
High 16-bit = 0x42A8, Low 16-bit = 0x0000
Combined into a 32-bit value (default Big-Endian): 0x42A80000
Binary representation: 0100 0010 1010 1000 0000 0000 0000 0000
IEEE 754 Decomposition:
• Sign bit (S) = 0 (positive)
• Exponent (E) = 10000101₂ = 133
• Fraction (M) = 01010000000000000000000₂
Plug into the IEEE 754 formula to get the decimal value:
84.0
